Produkt splotu

W matematyce The produkt splotu jest operatorem dwuliniowo i przemienne Produkt ogólnie oznaczony „ $*$ ”, który do dwóch funkcji $f$ i $g$ tej samej domeny nieskończonej odpowiada innej funkcji „ $f$ $*$ $g$ ” w tym obszarze, który w dowolnym punkt tej jednej jest równy całce w całej dziedzinie (lub sumie, jeśli jest dyskretna ) jednej z dwóch funkcji wokół tego punktu, ważonej przez drugą funkcję wokół początku - dwie funkcje są przechodzące w przeciwnych kierunkach od siebie nawzajem (niezbędne do zagwarantowania przemienności).

Iloczyn splotu uogólnia ideę ruchomej średniej i jest matematyczną reprezentacją pojęcia filtru liniowego . Dotyczy to równie dobrze danych czasowych ( na przykład w przetwarzaniu sygnałów ), jak i danych przestrzennych (w przetwarzaniu obrazu ). W statystykach używamy bardzo podobnego wzoru do definiowania korelacji krzyżowej .

Definicja iloczynu splotu

Iloczyn splotu dwóch rzeczywistych lub zespolonych funkcji $f$ i $g$ jest inną funkcją, która jest ogólnie oznaczana jako „ $f * g$ ” i która jest zdefiniowana przez:

{\ Displaystyle (f \ ast g) (x) = \ int _ {- \ infty} ^ {+ \ infty} f (xt) g (t) \, \ mathrm {d} t = \ int _ {- \ infty} ^ {+ \ infty} f (t) g (xt) \, \ mathrm {d} t}

I znowu, dla sekwencji (o wymianie środka Lebesgue'a przez środek zliczania )

{\ Displaystyle (f \ ast g) (n) = \ suma _ {m = - \ infty} ^ {\ infty} {f (nm) g (m)} = \ suma _ {m = - \ infty} ^ {\ infty} {f (m) g (nm)}}

Jeśli chodzi o serie, mówimy o iloczynie Cauchy'ego (ale w dalszej części będziemy używać tylko wersji „ciągłej”).

Możemy potraktować tę formułę jako uogólnienie idei średniej ruchomej .

Aby ta definicja była znacząca, $f$ i $g muszą$ spełniać pewne hipotezy; na przykład, jeśli te dwie funkcje są całkowalne w sensie Lebesgue'a (tj. są mierzalne, a całka ich modułu jest skończona), ich iloczyn splotu jest zdefiniowany dla prawie wszystkich x i sam jest całkowalny. Mówiąc bardziej ogólnie, jeśli $f \in L p$ i $g \in L q$ oraz z , to $f$ $*$ $g$ $\in L$ $r$ : por. „ Nierówność Younga za splot ”. ${\ Displaystyle {\ Frac {1} {p}} + {\ Frac {1} {q}} = 1 + {\ Frac {1} {r}}}$ ${\ Displaystyle p, q, r \ w [1, + \ infty]}$

Właściwości produktu splotowego

Właściwości algebraiczne

Iloczyn splotu jest dwuliniowy , asocjacyjny i przemienny :

{\ Displaystyle f \ ast (g + \ lambda h) = (fa \ ast g) + \ lambda (f \ ast h)}

(dla dowolnego skalara

λ

);

{\ Displaystyle (fa \ ast g) \ ast h = fa \ ast (g \ ast h)}

;

{\ displaystyle f \ ast g = g \ ast f}

. Demonstracja

Iloczyn splotu jest dystrybucyjny w stosunku do dodania:

${\ Displaystyle {\ rozpocząć {wyrównane} (f \ ast (g + h)) (x) & {\ stackrel {\ mathrm {def.}} {=}} \ int _ {- \ infty} ^ {+ \ infty} f (xt) (g (t) + h (t)) \, \ mathrm {d} t \\ & = \ int _ {- \ infty} ^ {+ \ infty} [f (xt) g ( t) + f (xt) h (t)] \, \ mathrm {d} t \\ & = \ int _ {- \ infty} ^ {+ \ infty} f (xt) g (t) \, \ mathrm {d} t + \ int _ {- \ infty} ^ {+ \ infty} f (xt) h (t) \, \ mathrm {d} t \\ & {\ stackrel {\ mathrm {def.}} { =}} (f \ ast g) (x) + (f \ ast h) (x). \ end {wyrównane}}}$

Iloczyn splotu jest asocjacyjny, gdy rozważa się funkcje całkowalne (do których ma zastosowanie twierdzenie Fubiniego ): ${\ Displaystyle {\ rozpocząć {wyrównane} ((f \ ast g) \ ast h) (r) & {\ stackrel {\ mathrm {def.}} {=}} \ int _ {- \ infty} ^ {+ \ infty} \ left (\ int _ {- \ infty} ^ {+ \ infty} f ((yx) -t) g (t) \, \ mathrm {d} t \ right) h (x) \, \ mathrm {d} x \\ & = \ int _ {- \ infty} ^ {+ \ infty} \ int _ {- \ infty} ^ {+ \ infty} f (yT) g (Tx) h (x) \ , \ mathrm {d} x \, \ mathrm {d} T \\ & = \ int _ {- \ infty} ^ {+ \ infty} f (yT) \ left (\ int _ {- \ infty} ^ { + \ infty} g (Tx) h (x) \, \ mathrm {d} x \ right) \, \ mathrm {d} T \\ & {\ stackrel {\ mathrm {def.}} {=}} ( f \ ast (g \ ast h)) (y) \ end {wyrównane}}}$ gdzie albo i . $T = x + t$ $t = Tx$ ${\ Displaystyle \ mathrm {d} t = \ mathrm {d} T}$
Iloczyn splotu jest przemienny. Można to łatwo zobaczyć, operując następującą zmianą zmiennej : ${\ Displaystyle {\ rozpocząć {wyrównane} (f \ ast g) (x) & {\ stackrel {\ mathrm {def.}} {=}} \ int _ {- \ infty} ^ {+ \ infty} f ( xt) g (t) \, \ mathrm {d} t \\ & = \ int _ {+ \ infty} ^ {- \ infty} f (T) g (xT) \, \ mathrm {d} (-T ) \\ & = \ int _ {- \ infty} ^ {+ \ infty} f (T) g (xT) \, \ mathrm {d} T \; \\ & {\ stackrel {\ mathrm {def.} } {=}} (g \ ast f) (x) \ end {aligned}}}$ gdzie $T = x - t$ , niech $t = x - T$ i $d t = d (- T )$ .

Pseudo-ring

Zbiór funkcji integrowalnych z dodaniem i iloczynem splotu tworzy zatem pseudo-pierścień , to znaczy niejednostkowy pierścień . Rzeczywiście, gdyby ten pierścień był jednolity, element jednostkowy $δ$ powinien sprawdzić (dla dowolnego $x$ i dowolnej funkcji $f$ ):

{\ Displaystyle f (x) = \ int _ {- \ infty} ^ {+ \ infty} f (t) \ delta (xt) \ \, \ mathrm {d} t}

Można łatwo sprawdzić, czy jest to możliwe tylko wtedy, gdy $δ$ jest rozkładem Diraca … który nie jest funkcją.

Naturalną podstawą dobrego uogólnienia iloczynu splotu jest teoria dystrybucji , ale nie jest ona omawiana w tym artykule. W artykule poświęconym rozkładom znajdziemy dokładną definicję iloczynu splotu w tym przypadku, a także studium jego głównych właściwości.

Zgodność z tłumaczeniami

Iloczyn splotu jest zgodny z tłumaczeniami czasowymi. Jeśli oznaczymy przez $τ h$ translację funkcji zdefiniowanych przez

{\ Displaystyle (\ tau _ {h} f) (x) = f (xh)}

więc

{\ Displaystyle (\ tau _ {h} f) \ ast g = \ tau _ {h} (f \ ast g).}

W większym ramach splotu działań ,

{\ displaystyle \ tau _ {h} f = \ delta _ {h} \ ast f}

gdzie $δ h$ oznacza masę Diraca w h , a zgodność z tłumaczeniami jest tylko bezpośrednią konsekwencją asocjatywności iloczynu splotu miar:

{\ Displaystyle (\ tau _ {h} f) \ ast g = (\ delta _ {h} \ ast f) \ ast g = \ delta _ {h} \ ast (f \ ast g) = \ tau _ { h} (f \ ast g).}

Tę właściwość należy również porównać z zastosowaniami produktów splotu do filtrowania .

Parytet

Splot następuje reguły znak dla parzystości funkcji :

f * g

jest parzyste (odp. nieparzyste), jeśli

f

g

mają tę samą parzystość (odp. Demonstracja

Oznaczmy przez $I$ inwolucji definicją i upewnij się, że . ${\ Displaystyle (jeśli) (x) = f (-x)}$ ${\ Displaystyle I (f \ ast g) = (jeśli) \ ast (Ig)}$

{\ Displaystyle {\ rozpocząć {wyrównane} (ja (f \ ast g)) (x) & = (f \ ast g) (- x) \\ & = \ int _ {- \ infty} ^ {+ \ infty } f (-xt) g (t) \, \ mathrm {d} t \\ & = \ int _ {- \ infty} ^ {+ \ infty} f (-x + u) g (-u) \, \ mathrm {d} u \\ & = \ int _ {- \ infty} ^ {+ \ infty} (If) (xu) (Ig) (u) \, \ mathrm {d} u \\ & = (( Jeśli) \ ast Ig) (x). \ End {aligned}}}

Ta własność w połączeniu z niezmienniczością w translacji pozwala udowodnić, że iloczyn splotu przez funkcję parzystą zachowuje osiowe symetrie funkcji:

Jeśli

g

jest parzyste i jeśli

f ( x - h ) = f (- x - h ),

( f * g ) ( x - h ) = ( f * g ) (- x - h )

. Demonstracja

Pierwsze równanie jest równoważne . Możemy wywnioskować ${\ Displaystyle \ tau _ {h} (f) (x) = \ tau _ {h} (f) (- x)}$

{\ Displaystyle ((\ tau _ {h} f) \ ast g) (x) = ((\ tau _ {h} f) \ ast g) (- x) = \ tau _ {h} (f \ ast g) (x) = \ tau _ {h} (f \ ast g) (- x)}

co jest ogłoszonym wynikiem.

Integracja produktu splotowego

Mamy (stosując twierdzenie Fubiniego ) wzór: ${\ Displaystyle \ int _ {- \ infty} ^ {+ \ infty} (f \ ast g) (t) \, \ mathrm {d} t = \ lewo (\ int _ {- \ infty} ^ {+ \ infty} f (t) \, \ mathrm {d} t \ right) \ left (\ int _ {- \ infty} ^ {+ \ infty} g (t) \, \ mathrm {d} t \ right). }$

Pochodzenie

W przypadku pojedynczej zmiennej, jeśli $f$ (na przykład) jest klasy $C 1$ i jeśli $f$ , $f '$ a $g$ należą do $L 1$ , a następnie

{\ displaystyle (f * g) '= f' * g}

Bardziej ogólnie w przypadku funkcji kilku zmiennych, które mamy

{\ Displaystyle {\ Frac {\ częściowe} {\ częściowe x_ {i}}} (f * g) = {\ Frac {\ częściowe f} {\ częściowe x_ {i}}} * g}

Iloczyn splotu i transformata Fouriera

Transformaty Fouriera produktu splotu uzyskuje się poprzez pomnożenie transformacji Fouriera funkcji:

jeśli $f$ i $g$ są całkowalne, to ${\ Displaystyle {\ mathcal {F}} (fa \ ast g) = {\ mathcal {f}} (f) {\ mathcal {f}} (g) ~;}$
jeśli $f$ jest całkowalne i jeśli $g$ jest całkowalne do kwadratu , również mamy

${\ Displaystyle {\ mathcal {F}} (fa \ ast g) = {\ mathcal {f}} (f) {\ mathcal {f}} (g) {\ tekst {w związku z tym}} f \ ast g = { \ mathcal {F}} ^ {- 1} \ left ({\ mathcal {F}} (f) {\ mathcal {F}} (g) \ right) ~;}$

jeśli $f$ i $g$ są całkowalne do kwadratu, to ${\ displaystyle f \ ast g = {\ mathcal {F}} ^ {- 1} \ lewo ({\ mathcal {F}} (f) {\ mathcal {F}} (g) \ prawej)}$

gdzie oznacza transformację Fouriera i odwrotną transformację Fouriera („twierdzenie o splotach”). ${\ mathcal {F}}$ ${\ displaystyle {\ mathcal {F}} ^ {- 1}}$

Wzory te są ograniczone do przestrzeni Schwartza , a następnie rozciągają się częściowo do transformacji Fouriera dla rozkładów umiarkowanych , stosowanej na przykład do splotu rozkładu temperowanego przez rozkład o zwartym nośniku . Mówiąc bardziej ogólnie, jeśli S i T są dwoma temperowanymi dystrybucjami , z których jeden jest splotem , to ich transformaty Fouriera są temperowanymi dystrybucjami, z których jeden jest mnożnikiem i weryfikują: ${\ Displaystyle {\ mathcal {F}} (S \ ast T) = {\ mathcal {F}} (S) {\ mathcal {F}} (T) {\ tekst {w związku z tym}} S \ ast T = { \ mathcal {F}} ^ {- 1} \ left ({\ mathcal {F}} (S) {\ mathcal {F}} (T) \ right).}$

W tym ujęciu rozkład Diraca ( neutralny konwektor ) i stała funkcja $1$ (neutralny mnożnik) są dwoma rozkładami umiarkowanymi (parami) przekształconymi od siebie przez Fouriera.

Głównym celem obliczania iloczynu splotu za pomocą transformacji Fouriera jest to, że operacje te są tańsze w czasie dla komputera niż bezpośrednie obliczenie całki.

Korzystanie z produktu konwolucji

Produkt splotu jest używany w przetwarzaniu sygnału przy użyciu filtrów ( dolnoprzepustowy , górnoprzepustowy , pasmowy ). Jeśli mamy przychodzący sygnał $e ( t )$ i element filtrujący o funkcji przenoszenia $h ( t ),$ to sygnał wyjściowy $s ( t )$ będzie splotem tych dwóch funkcji: ${\ displaystyle s = e \ ast h}$ (iloczyn splotu) i $S ( f ) = E ( f ) H ( f )$ (iloczyn prosty dwóch funkcji)gdzie $E ( m )$ , $S ( f )$ i $H ( f )$ są transformaty Fouriera w funkcji czasu $e ( t )$ , $s ( t )$ oraz $h ( t )$ .
W krystalografii , twierdzenie splotu jest stosowany w metodach bezpośredniego dla ustalania stadium z czynników strukturalnych podczas określania struktury kryształu .
Prawdopodobieństwo, że gęstość prawdopodobieństwa sumy dwóch niezależnych rzeczywistych zmiennych losowych (gęstości) jest iloczynem splotu gęstości prawdopodobieństwa tych dwóch zmiennych niezależnych, co widać na podstawie zmiany zmiennych .
Innym zastosowaniem produktów splotu jest dziedzina mechaniki kwantowej, w której produkty splotu są wytwarzane z funkcji fal biustonoszowych i ketowych .
Ogólnie rzecz biorąc, możemy zapisać liniowe równania różniczkowe odpowiadające wielu problemom fizycznym w postaci iloczynu splotu operatora przez funkcję opisującą układ. Następnie możemy rozwiązać problem w sposób ogólny, określając odwrotność splotu operatora (zwaną funkcją Greena ). Joseph Fourier był początkiem tej metody, kiedy próbował rozwiązać równanie ciepła . Jego nowoczesne sformułowanie musiało czekać na pojawienie się teorii dystrybucji wprowadzonej przez Laurenta Schwartza .
Iloczyn splotu uogólnia wiele algebr grupy, na przykład algebr grupy skończonej . Jeśli ponadto grupa jest abelowa, to teoria analizy harmonicznej na skończonej grupie abelowej umożliwia ustalenie wszystkich klasycznych wyników iloczynu splotu.
W głębokiej nauki , operatorzy splotu są banki filtrów o sieciach neuronowych splotowych na wizji komputerowej i przetwarzania języka naturalnego .

Iloczyn splotu miar

Splot miar na linii rzeczywistej

Rozszerzając, możemy zdefiniować iloczyn splotu dwóch miar na podstawie następującej interpretacji probabilistycznej: kiedy prawa prawdopodobieństwa $μ$ i $ν$ dwóch niezależnych rzeczywistych zmiennych losowych nie mają gęstości w odniesieniu do miary Lebesgue'a , to prawo ich sumy jest splatanie z $ľ$ o $v$ , oznaczoną $μ$ $*$ $ν$ i zdefiniowane dla każdej części Borel $a$ o o ${\ Displaystyle (\ mathbb {R}, {\ mathcal {B}} (\ mathbb {R}))}$ $\ mathbb {R},$

\ mu \ ast \ nu (A) = \ int _ {{\ mathbb {R} ^ {2}}} \ 1_ {A} (x + y) \, \ mu ({\ mathrm d} x) \, \ nu ({\ mathrm d} y).

Całka funkcji θ względem miary $μ * ν$ jest dana $wzorem$

\ int _ {{\ mathbb {R}}} \ \ theta (s) \, (\ mu \ ast \ nu) ({\ mathrm d} s) \ = \ \ int _ {{\ mathbb {R} ^ {2}}} \ \ theta (x + y) \, \ mu ({\ mathrm d} x) \, \ nu ({\ mathrm d} y).

Iloczyn splotu $μ * ν$ jest miarą obrazu za pomocą funkcji φ , określonej przez $φ$ $($ $x$ $,$ $y$ $) =$ $x$ $+$ $y$ , miary iloczynu $μ$ $\otimes$ $ν$ . W szczególności, jeśli zarówno $μ, jak$ i $ν$ mają gęstości, odpowiednio $f$ i $g$ , w odniesieniu do miary Lebesgue'a, to $μ$ $*$ $ν$ ma również gęstość w stosunku do miary Lebesgue'a, a jedna z jej gęstości jest $f$ $*$ $g$ . $\ mathbb {R} ^ {2}$

Splot miar na grupie przemiennej

Tę definicję iloczynu splotu można natychmiast rozszerzyć do przemiennej grupy topologicznej $( G , end)$ wyposażonej w plemię borelijskie : dla dowolnej borelijskiej części $A$ z $G$ ,

{\ Displaystyle \ mu \ ast \ nu (A) = \ int _ {G ^ {2}} \ 1_ {A} (x \ oplus y) \, \ mu (\ operatorname {d} x) \, \ nu (\ mathrm {d} y).}

Całka funkcji θ względem miary $μ * ν$ jest dana $wzorem$

{\ Displaystyle \ int _ {G} \ \ theta (s) \, (\ mu \ ast \ nu) (\ mathrm {d} s) \ = \ \ int _ {G ^ {2}} \ \ theta ( x \ oplus y) \, \ mu (\ mathrm {d} x) \, \ nu (\ mathrm {d} y).}

Pojęcie miary Haara grupy $G$ jest następnie zapisane w postaci iloczynu splotu: $μ$ jest miarą Haara $G$ wtedy i tylko wtedy, gdy dla dowolnego elementu $g$ z $G$ ,

{\ displaystyle \ delta _ {g} \ ast \ mu = \ mu.}

Jeśli grupa nie jest przemienna, nadal możemy zdefiniować produkt splotu, określając splot w lewo lub w prawo.

Mówiąc bardziej ogólnie, możemy zdefiniować produkt splotu dla akcji grupowej . Niech $G będzie$ mierzalną grupą działającą na mierzalnej przestrzeni K , o zanotowanym działaniu. i są dopasowane do $μ$ $G$ i K dopasowane do $ν$ . Iloczyn splotu określamy wzorem

{\ Displaystyle \ mu * \ nu (a) = \ int _ {K} \ int _ {G} {\ mathsf {1}} _ {A} (gx) \, \ mu (\ mathrm {d} g) \, \ nu (\ mathrm {d} x)}

gdzie do zmierzenia część K .

Jest to miara K . Jeśli K = G i jeśli akcją jest mnożenie (lub mnożenie w lewo lub w prawo, jeśli grupa nie jest przemienna), to znajdujemy iloczyn splotu na grupach opisanych powyżej.

Podejście spopularyzowane

Najprostszym sposobem przedstawienia iloczynu splotu jest rozważenie funkcji Diraca δ $δ a ( x )$ ; ta „funkcja” jest warta 0, jeśli x ≠ a, a jej całka jest warta 1. Może się to wydawać sprzeczne z intuicją, ale możemy to sobie wyobrazić jako ograniczenie szeregu funkcji, krzywych dzwonowych lub prostokątów o tej samej powierzchni 1, ale coraz cieńsze (a zatem coraz wyższe); gdy szerokość krzywych dąży do 0, jego wysokość dąży do + ∞, ale pozostaje pole równe 1. Ze względów praktycznych, często stanowią Diraca kija umieszczonym na i wysokości 1.

Iloczyn splotu przez dirac $δ a$ odpowiada translacji funkcji początkowej o wartość a

f \ ast \ delta _ {a} (x) = f (xa)

Iloczyn splotu funkcji przez diraca

Widzimy, że δ 0 pozostawia niezmienną funkcję, jest to neutralny element iloczynu splotu

f \ ast \ delta _ {0} (x) = f (x-0)

Jeśli teraz rozważymy iloczyn splotu przez ważoną sumę dwóch diraków ( $α δ a + β δ b$ ), otrzymamy superpozycję dwóch przesuniętych krzywych.

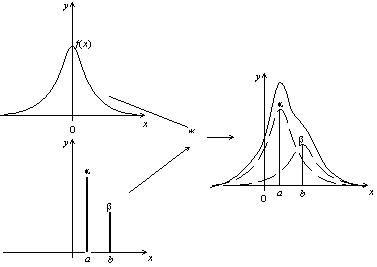
Iloczyn splotu funkcji przez sumę ważoną dwóch diraków

Rozważmy teraz funkcję bramki P a, b ; jest to funkcja o wartości 1 / ( ba ) między a i b oraz 0 w innych miejscach (jej całka jest warta 1). Ta funkcja może być postrzegana jako następstwo diraków. Splot $f$ przez P a, b zostanie zatem uzyskany przez przeciągnięcie $f$ przez przedział [ a ; b ]. Uzyskujemy „powiększenie” $f$ .

Iloczyn splotu funkcji przez funkcję bramkową

Jeśli teraz rozważymy jakąkolwiek funkcję $g$ , możemy zobaczyć $g$ jako ciąg diraków ważony wartością $g$ w rozważanym punkcie. Iloczyn splotu $f$ na $g$ uzyskuje się więc przeciągając funkcję $f$ i rozszerzając ją zgodnie z wartością $g$ .

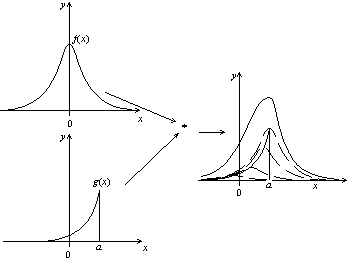
Iloczyn splotu funkcji według dowolnej funkcji

Iloczyn splotu i filtrowania

Iloczyn splotu jest powiązany z pojęciem filtrowania pod dwoma warunkami, a mianowicie liniowością i niezależnością filtra względem czasu ( system niezmienny ). Z tych dwóch warunków można skonstruować operator splotu. Splot odpowiada odpowiedzi filtra na dane wejście (zaznaczone $e ( t )$ ). Filtr charakteryzuje się całkowicie odpowiedzią impulsową $h ( t )$ . Umieść w równaniu odpowiedź filtra $s ( t ) = { h * e } ( t )$ .

Konstrukcja operatora splotu jest opracowana w następujący sposób. Przede wszystkim interesują nas dwa warunki nałożone na filtr. Oznaczamy przez $f ( e )$ filtrowanie wykonywane przez filtr na wejściu e . Liniowość filtra oznacza, że:

f (\ lambda e) = \ lambda f (e)

f (e_ {1} + e_ {2}) = f (e_ {1}) + f (e_ {2})

Można zauważyć, że odpowiedź filtra na sygnał zerowy wynosi zero. Niezależność czasu podsumowuje:

f (e ^ {d}) = (f (e)) ^ {d}

gdzie $e d$ jest sygnałem $e$ opóźnionym o wielkość $d$ .

Stamtąd możemy zbudować odpowiedź liniowego i niezależnego od czasu filtra na wejściu $e ( t )$ . W istocie, jako że filtr nie jest liniowa, można rozłożyć sygnał $e ( t )$ , na oddzielne części, za pomocą zestawu sygnałów $e I$ o zwartej rozłączne podpory takie, że . Każda część sygnału jest wprowadzana do filtra, a następnie sumowane są różne odpowiedzi. Zatem filtrowanie woli: . Ten czasowy rozkład $e$ $($ $t$ $)$ można przeprowadzić rekurencyjnie na sygnałach $e$ $i$ $($ $τ$ $)$ . Na koniec otrzymujemy serię sygnałów, których wsparcie sprowadza się do pewnego momentu. Te sygnały, elementarne, ponieważ nie można ich rozłożyć w czasie, każdy odpowiada rozkładowi Diraca $δ$ $($ $t$ $-$ $τ$ $)$ wyśrodkowanym w $τ$ z amplitudą $e$ $($ $τ$ $)$ , impuls zapisuje się $δ$ $($ $t$ $-$ $τ$ $)$ $e$ $($ $τ$ $)$ . Wystarczy dodać wszystkie impulsy wzdłuż zmiennej $τ,$ aby otrzymać sygnał $e$ $($ $t$ $)$ : $e (t) = \ Sigma _ {i} e_ {i} (t)$ $f (e) = \ Sigma _ {i} f (e_ {i})$

{\ Displaystyle e (t) = \ int \ delta (t- \ tau) e (\ tau) \ \, \ mathrm {d} \ tau}

Zastosujemy operację filtrowania do $e ( t )$ . Ponieważ filtr jest liniowy i niezależny od czasu, mamy:

{\ Displaystyle {\ rozpocząć {wyrównane} f (e) & = \ int f (\ delta (t- \ tau) e (\ tau)) \ \ mathrm {d} \ tau \\ & = \ int e ( \ tau) f (\ delta (t- \ tau)) \, \ mathrm {d} \ tau & {\ text {(liniowość)}} \\ & = \ int e (\ tau) (f \ circ \ delta ) (t- \ tau) \, \ mathrm {d} \ tau & {\ text {(niezależność czasowa).}} \ end {aligned}}}

Odpowiedź filtra $f$ na impuls $δ ( t )$ nazywana jest odpowiedzią impulsową filtra $h ( t )$ . Wreszcie mamy:

{\ Displaystyle f (e) = \ int e (\ tau) h (t- \ tau) \ \ mathrm {d} \ tau}

który jest niczym innym jak produktem splotu.

Podsumowując: jeśli filtr jest liniowy i niezależny od czasu, to jest on całkowicie scharakteryzowany przez swoją odpowiedź $h ( t ),$ a odpowiedź filtru na wejściu $e ( t )$ jest podana przez operator splotu.

Kolejna podstawowa konkluzja filtrów liniowych i niezależnych od czasu: jeśli wprowadzimy sygnał $e ( t ) = e 2 π j ft$ , sygnał wyjściowy będzie wyglądał następująco:

{\ Displaystyle {\ rozpocząć {wyrównane} s (t) & = \ int \ mathrm {e} ^ {2 \ pi \ jmath f \ tau} h (t- \ tau) \ \, \ mathrm {d} \ tau \ \ & = \ int \ mathrm {e} ^ {2 \ pi \ jmath f (t- \ tau)} h (\ tau) \, \ mathrm {d} \ tau \\ & = \ mathrm {e} ^ { 2 \ pi \ jmath ft} \ int \ mathrm {e} ^ {- 2 \ pi \ jmath f \ tau} h (\ tau) \, \ mathrm {d} \ tau \\ & = \ mathrm {e} ^ {2 \ pi \ jmath ft} H (f). \ End {wyrównane}}}

Sygnał $s ( t )$ będzie również sygnałem o postaci $e 2 π j ft$ do współczynnika $H ( f )$ . Czynnik ten nie jest niczym innym niż transformaty Fouriera z $h ( t )$ .

Uwagi i odniesienia

Zobacz też

Powiązane artykuły

Bibliografia

Marc Briane i Gilles Pagès, Teoria integracji: splot i transformata Fouriera , Paryż, Vuibert ,2012, 365 s. ( ISBN 978-2-311-00738-1 )

Linki zewnętrzne

( fr ) Animacja z Johns Hopkins University wyjaśniająca graficznie splot
Viva la Convolution : zastosowanie splotu do akustyki