Quadric

W matematyce , a Quadric lub kwadratowy powierzchni , to powierzchnia zaspokojenia wielomianu kartezjański równanie stopnia 2 z trzema zmiennymi (ogólnie zauważyć x , y i Ż ) kształtki

Wx2+by2+VSz2+2reyz+2mixz+2faxy+solx+H.y+jaz+jot=0{\ Displaystyle Ax ^ {2} + By ^ {2} + Cz ^ {2} + 2Dyz + 2Exz + 2Fxy + Gx + Hy + Iz + J = 0}.

Powierzchnie te są klasyfikowane za pomocą zredukowanego równania w ortonormalnym układzie współrzędnych dostosowanym do geometrii euklidesowej oraz w dziewięciu klasach niezdegenerowanych , aż do transformacji liniowej w geometrii afinicznej . Można je również badać w ramach geometrii rzutowej , co całkowicie upraszcza i ujednolica wyniki.

Ich płaskie sekcje są stożkowe .

Definicja jest uogólniona w wyższym wymiarze za pomocą pojęcia afinicznego kwadratu , hiperpowierzchni , charakteryzowanej jako miejsce anulowania  (in) wielomianu stopnia 2, nawet na innym korpusie współczynników niż w przypadku liczb rzeczywistych .

Klasyfikacja

Prezentacja głównych kwadryk

Niezdegenerowane kwadryki są opisane poniżej na podstawie ich zredukowanych równań w odpowiedniej ramie ortonormalnej.

elipsoidy	x2w2+y2b2+z2vs2-1=0{\ Displaystyle {\ Frac {x ^ {2}} {a ^ {2}}} + {\ Frac {y ^ {2}} {b ^ {2}}} + {\ Frac {z ^ {2} } {c ^ {2}}} - 1 = 0 \,} ,
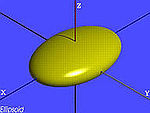
Jeden arkusz hiperboloidy (H1)	x2w2+y2b2-z2vs2-1=0{\ Displaystyle {\ Frac {x ^ {2}} {a ^ {2}}} + {\ Frac {y ^ {2}} {b ^ {2}}} - {\ Frac {z ^ {2} } {c ^ {2}}} - 1 = 0 \,} ,
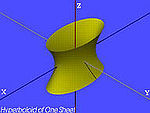
Hiperboloid dwuwarstwowy (H2)	x2w2+y2b2-z2vs2+1=0{\ Displaystyle {\ Frac {x ^ {2}} {a ^ {2}}} + {\ Frac {y ^ {2}} {b ^ {2}}} - {\ Frac {z ^ {2} } {c ^ {2}}} + 1 = 0 \,} ,
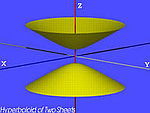
Eliptyczny paraboliczną (PE),	x2w2+y2b2=z{\ Displaystyle {\ Frac {x ^ {2}} {a ^ {2}}} + {\ Frac {y ^ {2}} {b ^ {2}}} = z \,} ,
Paraboloid hiperboliczny (PH)	x2w2-y2b2=z{\ Displaystyle {\ Frac {x ^ {2}} {a ^ {2}}} - {\ Frac {y ^ {2}} {b ^ {2}}} = z \,} ,
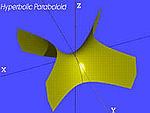
Eliptyczny podstawa stożka	x2w2+y2b2-z2vs2=0{\ Displaystyle {\ Frac {x ^ {2}} {a ^ {2}}} + {\ Frac {y ^ {2}} {b ^ {2}}} - {\ Frac {z ^ {2} } {c ^ {2}}} = 0 \,} ,
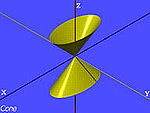
Eliptycznego cylindra	x2w2+y2b2-1=0{\ Displaystyle {\ Frac {x ^ {2}} {a ^ {2}}} + {\ Frac {y ^ {2}} {b ^ {2}}} - 1 = 0 \,} ,
Hiperboliczny cylindra	x2w2-y2b2-1=0{\ Displaystyle {\ Frac {x ^ {2}} {a ^ {2}}} - {\ Frac {y ^ {2}} {b ^ {2}}} - 1 = 0 \,} ,
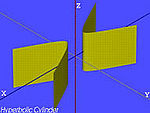
Paraboliczny cylindra	x2=2py{\ Displaystyle \ Displaystyle {x ^ {2} = 2py}} .

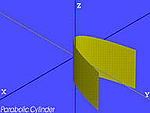
Generalna klasyfikacja

Równanie powierzchni można zapisać:

Q(x,y,z)+solx+H.y+jaz+jot=0 {\ Displaystyle Q (x, y, z) + Gx + Hy + Iz + J = 0 ~}

gdzie Q oznacza formę kwadratową

Q(x,y,z)=Wx2+by2+VSz2+2reyz+2mixz+2faxy {\ Displaystyle Q (x, y, z) = Ax ^ {2} + By ^ {2} + Cz ^ {2} + 2Dyz + 2Exz + 2Fxy ~}

matryca:

MQ=(WfamifabremireVS){\ Displaystyle M_ {Q} = {\ rozpocząć {pmatrix} A & F & E \\ F & B & D \\ E & D & C \ end {pmatrix}}}

których wszystkie wartości własne są rzeczywiste, ponieważ ta macierz jest prawdziwie symetryczna .

Podpisanie formularza kwadratowego jest parą (p, q) , gdzie P jest liczbą ściśle dodatnich wartości własnych Q i Q przez liczbę ściśle ujemnych wartości własnych. Ranga Q jest wtedy p + q . Z definicji kwadratu, rząd Q nie może wynosić zero. O tym, że podpis formy kwadratowej nie zależy od wyboru wybranej podstawy, świadczy prawo bezwładności Sylwestra .

Kiedy ranga jest równa 3, kwadryka przyjmuje środek symetrii.

Ranga	Podpis	Nie zdegenerowany quadric	Zdegenerowany quadric
3	(3,0) lub (0,3)	elipsoida	∅{\ displaystyle \ varnothing} lub punkt
	(2,1) lub (1,2)	hiperboloida z 1 lub 2 warstwami lub stożkiem
2	(2,0) lub (0,2)	eliptyczny, paraboloidalny lub eliptyczny cylinder	∅{\ displaystyle \ varnothing} lub prawo
	(1, 1)	hiperboliczny paraboloid lub hiperboliczny cylinder	spotkanie dwóch planów
1	(1,0) lub (0,1)	cylinder paraboliczny	∅{\ displaystyle \ varnothing} lub plan lub połączenie dwóch planów

Demonstracja

Aby uprościć, współrzędne zawsze będzie zauważyć, x , y i z, po różnych zmianach ortonormalnych punktów odniesienia, które następują.

Matryca postaci kwadratowej czyste wartości znamionowe , , jest diagonalized pomocą ortogonalną macierz transformacji. W nowym ortonormalnym układzie współrzędnych zapisywane jest równanie powierzchni α {\ displaystyle \ alpha ~}β {\ displaystyle \ beta ~}γ {\ displaystyle \ gamma ~}

αx2+βy2+γz2+px+qy+rz=k {\ Displaystyle \ alfa x ^ {2} + \ beta y ^ {2} + \ gamma z ^ {2} + px + qy + rz = k ~}.

Na przykład , gdy jedna z wartości własnych jest różna od zera, można wyśrodkować odpowiednią współrzędną: α {\ displaystyle \ alpha ~}

αx2+px=α((x+p2α)2-(p2α)2){\ Displaystyle \ alfa x ^ {2} + px = \ alfa ((x + {\ Frac {p} {2 \ alfa}}) ^ {2} - ({\ Frac {p} {2 \ alfa}} ) ^ {2})}

co sprowadza się do wykonania tłumaczenia lub zmiany pochodzenia układu odniesienia.

• Gdy ranga jest równa trzy, trzy wartości własne nie są zerowe; w nowym ortonormalnym układzie współrzędnych równanie wygląda następująco:

αx2+βy2+γz2=K. {\ Displaystyle \ alfa x ^ {2} + \ beta y ^ {2} + \ gamma z ^ {2} = K ~}.

• • jeśli podpis jest wart (3,0) lub (0,3), trzy wartości własne mają ten sam znak. Jeśli K wynosi zero, jest to punkt; w przeciwnym razie jest elipsoidą, jeśli K ma znak wartości własnych, aw przeciwnym razie pustego zbioru.
  • jeśli sygnatura jest warta (2,1) lub (1,2), dwie wartości własne mają ten sam znak, który powiemy tutaj jako większość; jeśli K wynosi zero, jest to stożek; w przeciwnym razie jest to hiperboloid z jednym arkuszem, jeśli K ma znak większości, a hiperboloid z dwoma arkuszami w innym przypadku.

• Gdy ranga jest równa dwa, na przykład jedna z wartości własnych jest równa zero i tylko jedna ; w nowym ortonormalnym układzie współrzędnych równanie wygląda następująco:γ {\ displaystyle \ gamma ~}

αx2+βy2+rz=K. {\ Displaystyle \ alfa x ^ {2} + \ beta y ^ {2} + rz = K ~}.

• • jeśli r jest niezerowe, otrzymujemy eliptyczny paraboloid, jeśli dwie niezerowe wartości własne mają ten sam znak, a paraboloid hiperboliczny w przeciwnym razie, ponieważ równanie jest zapisane:

αx2+βy2=-r(z-K.r{\ Displaystyle \ alfa x ^ {2} + \ beta y ^ {2} = - r (z - {\ Frac {K} {r}}}).

• • jeśli r jest równe zero, a K jest równe zero, jest to suma dwóch płaszczyzn, jeśli niezerowe wartości własne mają przeciwny znak, a jeśli nie, to linia prosta;
  • jeśli r jest równe zero i K niezerowe, jest to cylinder hiperboliczny, jeśli niezerowe wartości własne mają przeciwny znak, a jeśli nie, to eliptyczny cylinder, gdy K jest znakiem niezerowych wartości własnych, oraz W przeciwnym razie jestem pusty.

• Gdy ranga jest równa jeden, na przykład tylko jedna wartość własna jest różna od zera ; w nowym ortonormalnym układzie współrzędnych równanie wygląda następująco:β {\ displaystyle \ beta ~}

βy2+px+qy=K.  {\ Displaystyle \ beta y ^ {2} + px + qy = K ~~},

następnie po ostatniej zmianie ortonormalnego układu współrzędnych

βy2+P.x=L  {\ Displaystyle \ beta y ^ {2} + Px = L ~~}.

Jeśli P jest równe zero, otrzymujemy płaszczyznę, jeśli L wynosi zero, oraz sumę dwóch płaszczyzn lub zbioru pustego, w zależności od tego, czy L jest znakiem, czy nie. W przeciwnym razie jest to cylinder paraboliczny. β{\ displaystyle \ beta}

Klasyfikacja w geometrii afinicznej

Klasyfikacja w geometrii rzutowej

Quadric w dowolnym wymiarze

Mówiąc bardziej ogólnie, w przestrzeni o wymiarze D, jeśli współrzędne przestrzeni są takie , ogólna kwadratura jest hiperpowierzchnią zdefiniowaną przez równanie algebraiczne: {x1,x2,...,xre}{\ Displaystyle \ {x_ {1}, x_ {2}, \ kropki, x_ {D} \}}

∑ja,jot=1reQja,jotxjaxjot+∑ja=1reP.jaxja+R=0{\ displaystyle \ sum _ {i, j = 1} ^ {D} Q_ {i, j} x_ {i} x_ {j} + \ sum _ {i = 1} ^ {D} P_ {i} x_ { i} + R = 0}

dla konkretnego wyboru Q, P i R.

Znormalizowane równanie dla niezdegenerowanego kwadratu wyśrodkowanego na początku ma postać:

∑ja=1re±xja2wja2=1{\ Displaystyle \ sum _ {i = 1} ^ {D} \ pm {x_ {i} ^ {2} \ ponad a_ {i} ^ {2}} = 1}

Aplikacje

W modelowaniu obrazu

Na powierzchnię równanie The Taylor-Young wzór zapewnia lokalną aproksymacji powierzchni przez Quadratic równania: z=fa(x,y) {\ Displaystyle z = f (x, y) ~}

p(x-w)+q(y-b)+12[r(x-w)2+2s(x-w)(y-b)+t(y-b)2]{\ Displaystyle p (xa) + q (yb) + {\ Frac {1} {2}} [r (xa) ^ {2} + 2s (xa) (yb) + t (yb) ^ {2}] }

z tak zwanymi notacjami Monge p=∂fa∂x(w,b),q=∂fa∂y(w,b),r=∂2fa∂x2(w,b),t=∂2fa∂y2(w,b),s=∂2fa∂x∂y(w,b).{\ Displaystyle p = {\ Frac {\ częściowe f} {\ częściowe x}} (a, b), q = {\ Frac {\ częściowe f} {\ częściowe y}} (a, b), r = { \ frac {\ częściowe ^ {2} f} {\ częściowe x ^ {2}}} (a, b), t = {\ frac {\ częściowe ^ {2} f} {\ częściowe y ^ {2}} } (a, b), s = {\ frac {\ częściowe ^ {2} f} {\ częściowe x \ częściowe y}} (a, b).}

To lokalne przybliżenie jest używane w modelowaniu obrazu, gdzie zapewnia interesujące wyniki.

Uwagi i odniesienia

1. André Warusfel , „Quadriques” , w Słowniku matematyki, algebry, analizy, geometrii , Encyclopædia Universalis i Albin Michel,1997.
2. Ani pusty, ani zredukowany do punktu, linii, płaszczyzny lub połączenia dwóch płaszczyzn.
3. Sylvie Philipp, Strukturalne modelowanie tekstury. Ekstrakcja pierwotnego ziarna i zasada jego umieszczania w Twelfth colloque Gretsi , Juan-les-Pins, 1988, Lire en ligne , s.  590 .
4. Alaa Mustafa, Wkład w badanie dyskretnych krzywizn i ich zastosowań , 2008 [teza].

Zobacz też

• Stożkowy

<img src="https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">