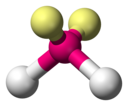
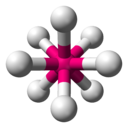
Teoria VSEPR

Teoria VSEPR (akronim angielskiego Valence Shell Electron Pair Repulsion , w języku francuskim RPECV  : „odpychanie elektronowych par warstwy walencyjnej”) jest metodą przewidzianą do przewidywania geometrii cząsteczek w oparciu o teorię odpychania elektronów do powłoka walencyjna . Jest również znany jako „teoria Gillespiego” (lub teoria Nyholma - Gillespiego ).

Pochodzenie

To brytyjski Nevil Sidgwick i Herbert Powell z Uniwersytetu Oksfordzkiego zaproponowali w 1940 roku korelację między geometrią molekularną a liczbą elektronów walencyjnych. W 1957 roku na University College w Londynie , Ronald Gillespie i Ronald Sydney Nyholm stosować ten pomysł wymyślić bardziej szczegółowy teorii. W 1958 roku Gillespie przeniósł się na McMaster University w Ontario i kontynuował rozwijanie i udoskonalanie teorii, dzięki czemu jest uważany za prawdziwego twórcę tej teorii. Metoda VSEPR jest kontynuacją idei wiązań chemicznych GN Lewisa (1916).

Wymagania wstępne i założenia

Metoda VSEPR opiera się na szeregu założeń, w szczególności dotyczących charakteru wiązań między atomami:

• atomy w cząsteczce są połączone parami elektronów;
• dwa atomy mogą być połączone więcej niż jedną parą elektronów. Mówimy wtedy o wielu linkach;
• niektóre atomy mogą mieć również pary elektronów, które nie są zaangażowane w wiązanie. Mówimy o niezobowiązujących dubletach  ;
• elektrony tworzące te wiążące lub niewiążące dublety wywierają na siebie odpychające siły elektryczne. Dlatego dublety są rozmieszczone wokół każdego atomu tak, aby zminimalizować wartości tych sił;
• niewiążące dublety zajmują więcej miejsca niż wiążące dublety;
• wiele wiązań zajmuje więcej miejsca niż pojedyncze.

Notacje

W dalszej części niniejszego, oraz, stosownie do sposobu VSEPR jeden zauważy centralnego atomu cząsteczki badanej .

Niewiążące dublety, to znaczy pary elektronów należące do centralnego atomu A i nie uczestniczące w wiązaniach, będą oznaczane przez E i ich liczbę m .

Spoiwa dublety, to znaczy pary elektronów są zaangażowane w wiązanie pomiędzy centralnym atomem A , a inny atom będą oznaczone X . Liczba dubletów wiążących będzie oznaczona przez n .

Uwaga: W odniesieniu do geometrii cząsteczki wielu wiążących jest podobny do pojedynczego wiązania, które to znaczy brak jest po prostu równa liczbie atomów przyłączone do A .

Proste cząsteczki, których geometrię można łatwo zdefiniować metodą VSEPR, mają zatem postać: AX n E m

Liczby odpychania

Metoda AX

Metoda AX umożliwia zdefiniowanie poniższych rysunków. Geometrie molekularne są nazywane tylko na podstawie pozycji atomów, a nie układu elektronów. Na przykład opis AX 2 E 2 jako wygiętej cząsteczki oznacza, że ​​trzy atomy AX 2 nie są w linii prostej, chociaż swobodne dublety pomagają określić geometrię.

Geometria

Dwuwymiarowe cząsteczki

Liczba steryczna m + n	Geometria bazowa 0 dublet niewiążący m = 0	1 niewiążący dublet m = 1	2 niewiążące dublety m = 2	3 niewiążące dublety m = 3
1	liniowy
2	liniowy	liniowy
3	trójkąt (płaszczyzna)	łokieć	liniowy
4	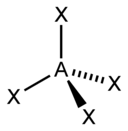czworościan	piramida trygonalna	łokieć	liniowy
5	bipiramidy trygonalne	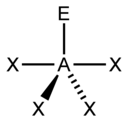huśtać się	Kształt litery T.	liniowy
6	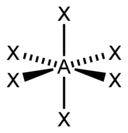oktaedr	piramida o podstawie kwadratu	kwadrat (plan)
7	pięciokątna dwupiramida	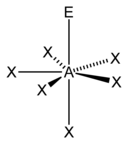piramida pięciokątna	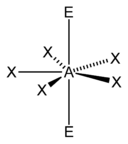pięciokąt (samolot)
8	kwadratowy antypryzmatyczny

Trójwymiarowe cząsteczki

Liczba dubletów m + n	Geometria bazowa 0 dublet niewiążący n = 0	1 niewiążący dublet n = 1	2 niewiążące dublety n = 2	3 niewiążące dublety n = 3
1	liniowy
2	liniowy	liniowy
3	trójkąt (płaszczyzna)	łokieć	liniowy
4	czworościan	piramida trygonalna	łokieć	liniowy
5	bipiramidy trygonalne	huśtawka	Kształt litery T.	liniowy
6	oktaedr	piramida o podstawie kwadratu	kwadrat (plan)
7	pięciokątna dwupiramida	piramida pięciokątna	pięciokąt (samolot)
8	kwadratowy antypryzmat
9	potknięty pryzmat trygonalny

Udoskonalenia modelu

Długość obligacji

Do tej pory uważaliśmy, że wszystkie wiązania między atomami są tej samej długości, są w przybliżeniu przybliżone i dalekie od rzeczywistości. Rzeczywiście, długości wiązań zmieniać się w zależności od węgla i typu wiązania (wiązanie pojedyncze, podwójne wiązania , potrójne wiązania , aromatyczne wiązania ...)

Możliwe jest eksperymentalne określenie odległości dzielącej dwa atomy, chociaż nie jest ona stała i zależy od ośrodka. Możesz jednak zdefiniować średnią wartość.

Metoda promienia kowalencyjnego

Jako pierwsze przybliżenie możemy asymilować atomy do kul, których promień jest równy promieniu kowalencji . Długość wiązania będzie wtedy wyrażona jako suma promieni kowalencyjnych atomów:

re=Rw+Rb{\ Displaystyle D = R_ {a} + R_ {b} \,}

z promieniem kowalencyjnym pierwszego atomu i promieniem kowalencyjnym drugiego atomu. Rw{\ displaystyle R_ {a}}Rb{\ displaystyle R_ {b}}

Metoda uwzględniająca różnicę elektroujemności

Ponieważ każdy atom ma inną elektroujemność , wpływa to również na długość wiązań; dokładniej, silna różnica w elektroujemności oznacza znaczne skrócenie wiązania. Możemy zatem ustalić następującą (empiryczną) formułę:

re=Rw+Rb-9×|δmi|{\ Displaystyle D = R_ {a} + R_ {b} -9 \ razy | \ delta _ {E} |}

z promieniem kowalencyjnym pierwszego atomu (w pikometrach ) i promieniem kowalencyjnym drugiego zaangażowanego atomu (w pikometrach), będącym różnicą elektroujemności między dwoma atomami (według skali Paulinga ). Rw{\ displaystyle R_ {a}}Rb{\ displaystyle R_ {b}}δmi{\ displaystyle \ delta _ {E}}

Wpływ wielu wiązań

Powyższe wzory pozwalają obliczyć długości pojedynczych wiązań przy stosunkowo niskim poziomie błędu. Na podstawie tych pomiarów można łatwo uzyskać wyniki wielu łączy.

Wiązanie podwójne znajduje się średnio 86% długości wiązania pojedynczego. Wiązanie potrójne zajmuje średnio 78% długości pojedynczego wiązania.

Na przykład wiązania aromatyczne, takie jak te obecne w cząsteczce benzenu , są pośrednie między wiązaniami pojedynczymi i podwójnymi:

• promień kowalencyjny węgla: 77 pm ;
• długość pojedynczego wiązania węgiel-węgiel (obliczona): 154 µm;
• długość wiązania podwójnego węgiel-węgiel (obliczona): 133 µm;
• długość wiązań węgiel-węgiel w cząsteczce benzenu (doświadczalnie): 140 µm.

Ograniczenia modelu

Nawet jeśli metoda VSEPR pozwala w zadowalający sposób przewidzieć geometrię prostych cząsteczek, dla których wybór centralnego atomu jest łatwy, jest trudniejsza do zastosowania i niewystarczająca, jeśli chodzi o przewidywanie geometrii bardziej złożonych cząsteczek. Na przykład wszystkie atomy cząsteczki etylenu (CH 2 = CH 2 ) znajdują się w tej samej płaszczyźnie, czego nie można przewidzieć za pomocą modelu. Bardziej zaawansowane modele pozwalają przezwyciężyć te niedociągnięcia, takie jak teoria orbitali molekularnych .

Ponadto cząsteczki, atomy, elektrony, nukleony nie są ustalonymi strukturami w czasie i przestrzeni. Ich względne pozycje zmieniają się w czasie i w zależności od ośrodka (patrz spektroskopia w podczerwieni - elektron ). Należy rozumieć, że teoria ta jest uproszczona w porównaniu z chemią kwantową i chemią cyfrową .

Uwagi i odniesienia

1. Sargent-Welch Scientific Canada Limited, Periodic Table of the Elements , Londyn, Ontario,1992
2. Bernard Valeur, Struktury molekularne , Paryż, Techniki inżynieryjne,2004

Linki zewnętrzne

• (fr) „  O geometrii cząsteczek  ” ( Archiwum • Wikiwix • Archive.is • Google • Co robić? )
• ( fr ) Na temat teorii VSEPR na stronie Uniwersytetu w Sheffield

<img src="https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1x1" alt="" title="" width="1" height="1" style="border: none; position: absolute;">