Beat (akustyczny)
W fizyce The bicie jest okresową modulacji sygnału składa się z superpozycji dwóch sygnałów bliskich częstotliwości . Termin pochodzi z akustyki ; w akustyce muzycznej dudnienie jest słyszalne, gdy dwie struny lub piszczałki wibrują z częstotliwościami od około 0,5 do 5 Hz .
Dudnienia można łatwo dostrzec, dostrajając instrument zdolny do podtrzymywania dźwięków. Strojenie dwóch nut jednocześnie daje specjalny efekt: tak długo, jak dwie nuty mają podobne, ale nie identyczne wysokości, różnica w częstotliwościach tworzy dudnienie; wynikowa nuta jest modulowana przez tremolo, ponieważ dźwięki interferują naprzemiennie konstruktywnie, a następnie destrukcyjnie. Gdy nuty zbliżają się do unisono, rytm zwalnia, a następnie znika. Zjawisko to jest również wykorzystywane do tworzenia basów organowych z dwoma nieco różnymi piszczałkami, dwukrotnie krótszymi niż to konieczne, których uderzenie na poziomie około dwudziestu herców tworzy nutę basową.
I odwrotnie, czysty dźwięk o modulowanej amplitudzie z tłumioną nośną wywołuje pulsujące wrażenie, o ile częstotliwość modulacji jest wystarczająco niska; kiedy to wzrasta, dostrzegamy dwie boczne linie widma. W ten sposób bada się selektywność częstotliwościową ucha.
W elektronice dudnienie jest używane do wykrywania synchronicznego .
Beat study
Fizyczny
Te dźwięki z instrumentów muzycznych zdolny do wytwarzania wynosi obejmują przede wszystkim fala formularz sinusoidalny , którego częstotliwość odpowiada na muzycznej boisko . Do analizy matematycznej wynika, że suma dwóch sinusoid równoważnych sinusoidy o częstotliwości równej ich średnia częstotliwość modulowanego w amplitudzie o sinusoidy o częstotliwości równej połowie różnicy w ich częstotliwości. Tak się dzieje, gdy mieszamy fale akustyczne dwóch nut.
Psychoakustyka rytmu
Jednak słuchanie mieszaniny dwóch dźwięków o częstotliwościach dostatecznie bliskich, aby usłyszeć dudnienie, pokazuje, że częstotliwość tego uderzenia jest różnicą częstotliwości dwóch dźwięków (a nie połową różnicy).
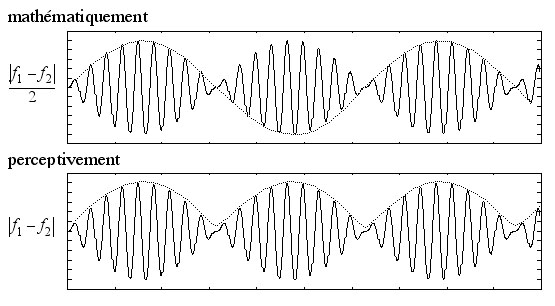
W rzeczywistości ucho ludzkie dostrzega różnice w natężeniu dźwięku mniejsze niż 10% i jest w stanie rozróżnić kilkaset częstotliwości dźwięku. Jako niezbędny odpowiednik, czas potrzebny na tę analizę czyni ją niewrażliwą na różnice w czasowej sytuacji składowych dźwięku.
Kiedy badamy falę dźwiękową powstałą z mieszaniny dwóch fal sinusoidalnych, zauważamy, że w dwóch momentach odległych od połowy okresu tremolo obliczonego matematycznie (połowy różnicy częstotliwości składowych), fale różnią się jedynie niewielkim przesunięciem czasowym (przesunięciem fazowym ) zależnym tylko od różnicy częstotliwości między składowymi. Nie słyszymy tej różnicy; dwie połowy okresu matematycznego wydają się identyczne, dlatego słyszymy nutę modulowaną tremolo częstotliwości równej różnicy między częstotliwościami składowych .
Przykład - suma z almost- :Przez dodanie sygnału odpowiadającego z częstotliwością 440 Hz, a drugi na prawie identycznym częstotliwości 443 Hz, sygnał uzyskuje się 441,5 Hz, a powłoka z rytmem otrzymanej częstotliwości 1,5 Hz
Granice zjawiska biciaZasady składania dwóch fal sinusoidalnych obowiązują niezależnie od częstotliwości każdej z nich. Wydają słyszalny rytm tylko wtedy, gdy
- natężenie dźwięku obu składników jest w przybliżeniu równe, tak aby jeden nie przesłaniał drugiego;
- rytm nie jest zbyt wolny (nie słychać okresu dłuższego niż 5 sekund);
- rytm nie jest zbyt szybki (gdy jego częstotliwość wzrasta, w końcu dostrzegamy te dwie składowe).
Kiedy nie odbieramy rytmu, znajdujemy się w bardziej ogólnym przypadku wynikowego dźwięku .
Wykorzystanie zjawiska trzepotania
Pokonaj harmoniczne
Dźwięki emitowane przez instrumenty muzyczne nie są czystymi sinusoidami emitowanymi przez instrumenty laboratoryjne. Są to kompozycje częstotliwości harmonicznych , to znaczy wielokrotności częstotliwości podstawowej przez liczbę całkowitą. Te części składowe można również łączyć, powodując, że dudnienia są słyszalne.
Przykład - uderzenie C 4 z G 4 :W umiarkowanym zakresie ( diapason 440)
- zrobić 4 ma częstotliwość 261,6 Hz
- piętro 4 ma częstotliwość 392 Hz
To jest piąty interwał . Współczynnik wynosi około 3/2
- trzecia harmoniczna C ma częstotliwość 784,8 Hz
- druga harmoniczna gruntu ma częstotliwość 784 Hz
Te dwie harmoniczne są słyszalne jako dźwięk 784,4 Hz z tremolo 0,8 Hz.
Strojenie instrumentów
Zjawisko dudnienia można bardzo dobrze usłyszeć, gdy człowiek stroi instrument smyczkowy (na przykład gitarę ): słychać wibrację dźwięku, wynikającą z mieszania się dźwięków emitowanych przez dwie zerwane struny. Jest to zjawisko, które umożliwia strojenie instrumentów muzycznych po prostu przez ucho: interwał jest czysty, gdy nie słychać więcej uderzeń.
W muzycznej tradycji muzyki zachodniej uważamy za czyste odstępy między nutami, których stosunek częstotliwości jest równy ułamkowi prostemu (3/2, 4/3 itd.). Jednak ze względów technicznych i estetycznych stosujemy skalę jednakowego temperamentu , w której pojedyncza proporcja rządzi różnicą między kolejnymi nutami: półton odpowiada częstotliwości około + 5,6%, tak że 12 półtonów tworzy oktawę . W tej skali, jak pokazał powyższy przykład C i G , relacje między nutami nie są już dokładnie harmoniczne . Metody strojenia wykorzystują liczenie uderzeń, aby umieścić nuty dokładnie w temperowanym interwale, w którym powinny znajdować się w instrumencie o stałym brzmieniu, takim jak fortepian .
Dokładność i rytm w muzyce zachodniej
Istnienie rozpoznanego beatu umożliwia wykonanie strojenia lub intonacji . Na przykład użycie jednakowego temperamentu powoduje bicie tercji (patrz artykuł: Poprawność tercji ).
Przykład - rytm tercji:W umiarkowanym zakresie ( diapason 440)
- F3 ma częstotliwość 174,6 Hz
- 3 ma częstotliwość 220 Hz
To jest główny trzeci interwał . Stosunek wynosi około 5/4
- piąta harmoniczna fa ma częstotliwość 873 Hz
- 4. harmoniczna ma częstotliwość 880 Hz
Te dwie harmoniczne są słyszalne jak dźwięk 876,5 Hz z tremolo 7 Hz.
Trzecia wielka nigdy nie jest używana czysto, z wyjątkiem muzyki dawnej ; jakość rytmu pozwala instrumentalistom upewnić się, że grają poprawnie .
Mniej spółgłoskowe, chociaż „właściwe” interwały, takie jak małe sekundy lub szóstki , mogą również wytwarzać dudnienia, które są nieodłączne dla ich natury. To jest powód ich słabej współbrzmienia .
Obliczenia i demonstracje
Sumowanie sinusoid o tej samej amplitudzie
Niech będzie sygnałem złożonym z sumy dwóch sinusoid
Charakterystyczną cechą każdego ze składników jest pulsacja ω, równa 2π × częstotliwość. Wiemy (patrz Trygonometria ) to
a więc
jeśli zapytamy
mamy
albo w całości
Suma dwóch sinusoid jest równoważna sinusoidie o częstotliwości równej średniej ich częstotliwości pomnożonej (lub modulowanej) przez sinusoidę o częstotliwości równej połowie różnicy ich częstotliwości.Sygnał ten jest okresowy tylko wtedy, gdy częstotliwości składowe są wielokrotnościami tej samej częstotliwości podstawowej przez liczby całkowite.
Sumowanie sinusoid o dowolnej amplitudzie
Jeśli teraz, dwie sinusoidy nie mają tej samej amplitudy:
Mamy takie same relacje jak poprzednio
Z tymi samymi zapisami, co poprzednio, mamy:
Różnica w fazach
Zaintrygowani różnicą między percepcją przez ucho, które słyszy uderzenie częstotliwości równej różnicy częstotliwości między składowymi, a wynikiem obliczeń matematycznych, staramy się porównać sygnał z pierwszej połowy okresu tremolo. fali sumarycznej (od czasu 0 do czasu 2π / ω d ) do sygnału drugiego półokresu, 2π / ω d później.
Więc zapytajmy
Mamy
Widzimy, że s ( t ' ) różni się od s ( t ) tylko różnicą faz (1+ ω m / ω d ) π, która zależy tylko od względnego odchylenia częstotliwości.
Ucho , którego narządy percepcji dźwięku, komórki sierść narządu Cortiego , zachowują się w sposób, jak filtry rezonatora o bardzo wąskim paśmie , nie można jednocześnie określić dokładną wysokość i czas. Konkretnego. Dlatego są z konieczności niewrażliwe na tę fazę. Nie jest więc zaskakujące, że nie odczuwamy żadnej różnicy między dwiema częściami matematycznego okresu uderzenia.
Załączniki
Bibliografia
- Antonio Fischetti , Wprowadzenie do akustyki , Paryż, Belin ,2001, 288 str. ( ISBN 2-7011-2683-5 ) , str. 21-21
- Mpaya Kitantou , „La perception auditive” , w: Denis Mercier (reżyseria), Le Livre des Techniques du Son, tom 1- Fundamental ideas , Paryż, Eyrolles ,1987, 1 st ed. ( prezentacja online )
- Mario Rossi , Audio , Lausanne, Presses Polytechniques et Universitaires Romandes,2007, 1 st ed.
Powiązane artykuły
- Jego wynik
- Dokładność tercji
- Mory w optyce , oferuje „wizualizację” z beatem.
- Consonance (muzyka)
Uwagi i odniesienia
- Richard Taillet , Loïc Villain i Pascal Febvre , Dictionary of Physics , Bruksela, De Boeck ,2013, s. 64 ; Międzynarodowa Komisja Elektrotechniczna , „103. Matematyka. Funkcje ” w CIE60050. Międzynarodowe słownictwo elektrotechniczne ,1987( czytaj online ) , s. 103-06-16 „beat”.
- Rossi 2007: 135.
- Kitantou 1987: 164
- Rossi 2007: 61 badań bije z fazerami .
- To stwierdzenie jest dające się udowodnić; aby wykazać prawdopodobieństwo tego , wystarczy zadać pytanie - Ile czasu zajmuje rozróżnienie między częstotliwością 100 Hz a inną częstotliwością 99 Hz wśród pewnej liczby dźwięków o nieznanych częstotliwościach?









