Pakiet logistyczny

W matematyce , A sekwencja logistyczna jest prosta sekwencja , ale nawrót który nie jest liniowa. Jego relacja powtarzania jest

xnie+1=μxnie(1-xnie), x0∈[0;1].{\ Displaystyle x_ {n + 1} = \ mu x_ {n} (1-x_ {n}), ~ x_ {0} \ w [0; 1].}

W zależności od wartości parametru μ (w [0; 4], aby zapewnić, że x pozostaje w [0; 1]), generuje sekwencję zbieżną, sekwencję poddaną oscylacjom lub sekwencję chaotyczną .

Ta kontynuacja, często cytowana jako przykład złożoności behawioralnej, która może wynikać z prostej nieliniowej zależności, została spopularyzowana przez biologa Roberta Maya w 1976 roku . Jednym z zastosowań pakietu logistycznego jest modelowanie wielkości populacji biologicznej na przestrzeni pokoleń.

To rozwiązanie w dyskretnym czasie od modelu Verhulst . Termin „logistyka” pochodzi z pracy Pierre'a François Verhulsta, który nazywa krzywą logistyczną ciągłym rozwiązaniem czasowym swojego modelu. W swojej pracy poświęconej temu zjawisku pisał w 1845 roku: „Tej krzywej damy termin logistyka” . Autor nie wyjaśnia swojego wyboru, ale „logistyka” ma ten sam pierwiastek co logarytm, a logistikos oznacza po grecku „obliczenie”.

Zachowanie zgodnie z μ

W modelu logistycznym weźmiemy pod uwagę, że zanotowana tutaj zmienna x n oznacza stosunek populacji gatunku do maksymalnej populacji tego gatunku (jest to liczba od 0 do 1). Zmieniając parametr μ obserwuje się kilka różnych zachowań:

Przypadek 0 ≤ µ ≤ 1 ludność wygasła.

W końcu gatunek umrze, niezależnie od populacji wyjściowej. Tj . lim+∞xnie=0{\ displaystyle \ lim _ {+ \ infty} x_ {n} = 0}

Przypadek 1 ≤ µ ≤ 3 wielkość populacji stabilizuje się.

• Jeśli 1 ≤ µ ≤ 2 , populacja ostatecznie ustabilizuje się wokół wartości , niezależnie od początkowej populacji. Innymi słowy .μ-1μ{\ displaystyle {\ frac {\ mu -1} {\ mu}}}lim+∞xnie=μ-1μ{\ Displaystyle \ lim _ {+ \ infty} x_ {n} = {\ Frac {\ mu -1} {\ mu}}}
• Jeśli 2 ≤ µ ≤ 3 , to również ustabilizuje się po pewnym czasie oscylacji. Szybkość zbieżności jest liniowa, z wyjątkiem µ = 3, gdzie jest bardzo mała.μ-1μ{\ displaystyle {\ frac {\ mu -1} {\ mu}}}

Przypadek 3 ≤ µ ≤ 3,57 wielkość populacji oscyluje między 2, 4, 8… wartościami (potęga 2).

• Jeśli 3 <µ ≤ 1 + √6 (około 3,45), w końcu oscyluje między dwiema wartościami, w zależności od µ, ale nie od populacji początkowej.
• Jeśli 3,45 <µ <3,54 (w przybliżeniu), w końcu oscyluje między czterema wartościami, ponownie zależnymi od µ, ale nie od populacji początkowej.
• Jeśli µ jest nieco większe niż 3,54, populacja kończy się oscylacją między ośmioma wartościami, a następnie 16, 32 i tak dalej. Przedział wartości µ prowadzących do takiej samej liczby oscylacji szybko maleje. Stosunek między dwoma z tych kolejnych przedziałów zbliża się za każdym razem , gdy stała Feigenbauma , δ = 4,669…. Żadne z tych zachowań nie zależy od początkowej populacji.

Przypadek 3,57 ≤ µ wielkość populacji jest chaotyczna , z pewnymi wyjątkami.

• Około μ = 3,57 , chaos zestawy w. Żadne oscylacje nie są jeszcze widoczne, a niewielkie różnice w początkowej populacji prowadzą do radykalnie różnych wyników.
• Większość wartości powyżej 3,57 ma charakter chaotyczny, ale istnieje kilka izolowanych wartości µ przy zachowaniu, które nie jest. Na przykład od 1 + √8 (około 3,82), mały przedział wartości µ wykazuje oscylację między trzema wartościami, a dla µ nieco większy, między sześcioma wartościami, a następnie dwunastoma i tak dalej. Inne przedziały oferują oscylacje między 5 wartościami itp. Wszystkie okresy oscylacji są obecne, również niezależnie od początkowej populacji.
• Powyżej µ = 4 stosunek populacji gatunku do populacji maksymalnej opuszcza przedział [0,1] i różni się prawie dla wszystkich wartości początkowych.

Opisane powyżej okresy oscylacji spełniają następującą zasadę. Rozważmy porządek Charkovskiego zdefiniowany na ściśle dodatnich liczbach całkowitych w następujący sposób:

3◃5◃7◃...◃2×3◃2×5◃2×7◃...◃2nie×3◃2nie×5◃2nie×7◃...{\ Displaystyle 3 \; \ triangleleft \; 5 \; \ triangleleft \; 7 \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 \ razy 3 \; \ triangleleft \; 2 \ razy 5 \; \ triangleleft \; 2 \ times 7 \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 ^ {n} \ times 3 \; \ triangleleft \; 2 ^ {n} \ times 5 \; \ triangleleft \; 2 ^ {n} \ times 7 \; \ triangleleft \; \ ldots} ◃2nie+1×3◃2nie+1×5◃...◃2nie◃2nie-1◃...◃22◃2◃1{\ Displaystyle \; \ triangleleft \; 2 ^ {n + 1} \ razy 3 \; \ triangleleft \; 2 ^ {n + 1} \ razy 5 \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 ^ {n} \; \ triangleleft \; 2 ^ {n-1} \; \ triangleleft \; \ ldots \; \ triangleleft \; 2 ^ {2} \; \ triangleleft \; 2 \; \ triangleleft \; 1 } Innymi słowy, najpierw umieszczamy nieparzyste, zaczynając od 3, w porządku rosnącym, potem nieparzyste pomnożone przez 2, potem przez 4 itd. a kończymy potęgami 2 w kolejności malejącej. Jeżeli wartość parametru µ odpowiada okresowi oscylacji n , to wszystkie liczby całkowite następujące po n w kolejności Charkowskiego odpowiadają okresom oscylacji, które już wystąpiły dla wartości parametru mniejszych niż µ . Zatem, ponieważ µ = 3,82 odpowiada okresowi 3, wszystkie możliwe okresy oscylacji wystąpiły już dla wartości µ między 0 a 3,82.

Schemat rozwidlenie  (w) stosuje się graficznie Podsumowując różne przypadki:

Komentarze

Kilka prostych argumentów i kilka wykresów częściowo rzuca światło na powyższe wyniki.

Grafika

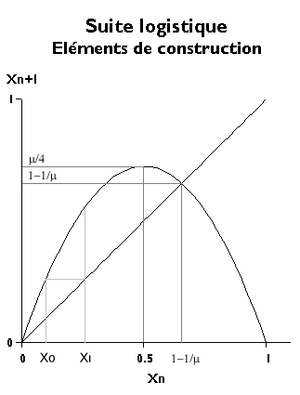
Ewolucję sekwencji logistycznej można przedstawić na płaszczyźnie ( x n , x n +1 ).

Podstawowe równanie przedstawia parabolę przechodzącą przez punkty odciętych 0 i 1 na osi poziomej. Aby wartości x n +1 nie stały się ujemne, konieczne jest zachowanie tylko łuku zawartego między tymi dwoma punktami; Stanowi to dla x n = 1 / 2 , o maksymalnej wartości μ / 4 . Ta wartość również musi zawierać się w przedziale od 0 do 1, stąd μ <4.

Jeśli sekwencja jest zbieżna, jej granica spełnia równanie granice x n +1 = granice x n . Ta możliwa granica, oznaczona przez x , jest rozwiązaniem równania kwadratowego

x=μx(1-x){\ Displaystyle x = \ mu x (1-x)}

i dlatego może przyjąć jedną lub drugą z wartości

x=0,x=1-1/μ{\ displaystyle x = 0, x = {1 - {1 / \ mu}}}

Aby opisać zachowanie ciągu, należy zacząć od odciętej x 0 , określić na paraboli wartość x 1, która jest następnie przekształcona w nową odciętą przechodzącą przez dwusieczną x n +1 = x n i powtórzyć te dwie operacje.

Obszary zbieżności

Dla pewnych wartości parametru μ sekwencja zachowuje się jak sekwencja klasyczna i zbliża się do jednej z dwóch możliwych granic. Podstawowe równanie można przepisać w postaci

xnie+1xnie=μ(1-xnie){\ Displaystyle {x_ {n + 1} \ ponad x_ {n}} = \ mu (1-x_ {n})}

Jeśli ciąg jest ograniczony ciągiem geometrycznym, który zmierza w kierunku 0. 0≤μ≤1{\ Displaystyle 0 \ równoważnik \ mu \ równoważnik 1}

Aby zobaczyć zachowanie w odniesieniu do drugiej możliwej granicy, wystarczy przeprowadzić zmianę zmiennej x n = u n + 1 - 1 / μ. Formuła wygląda następująco:

unie+1+1-1/μunie+1-1/μ=1-μunie{\ Displaystyle {{u_ {n + 1} + 1-1 / \ mu} \ ponad {u_ {n} + 1-1 / \ mu}} = 1- \ mu u_ {n}}

W tym przypadku, warunki zbieżności wymaga, aby drugi człon jest od -1 do +1: . 1≤μ≤3{\ displaystyle 1 \ leq \ mu \ leq 3}

Sprawdzamy, czy jeśli u n jest bliskie granicy 1 - 1 / μ, to 1-μ u n jest bliskie 2 - μ, a u n dąży do swojej granicy zwiększając wartości, jeśli μ jest mniejsze niż 2, o naprzemienne wartości, jeśli jest większe niż 2.

Rozwidlenia

W poprzednim akapicie wzór powtarzalności postaci x n +1 = f ( x n ) umożliwił uzyskanie pierwszych atraktorów poprzez poszukiwanie możliwej granicy zgodnej z równaniem x = f ( x ).

Kiedy μ staje się większe niż 3, musimy poszukać rozwiązania równania x = f ( f ( x )). Prowadzi to do równania czwartego stopnia, które naturalnie ma już znane korzenie - ale nie są one już atraktorami - i parę nowych korzeni. 0,1-1μ{\ Displaystyle 0,1 - {\ Frac {1} {\ mu}}}

12(1+μμ±1μμ2-2μ-3){\ Displaystyle {1 \ ponad 2} \ lewo ({1+ \ mu \ ponad \ mu} \ pm {1 \ ponad \ mu} {\ sqrt {\ mu ^ {2} -2 \ mu -3}} \ dobrze)}

Nie ma już zbieżności: pojawia się cykl graniczny. Wynik iteracji na przemian przełącza się z jednego z dwóch ostatnich pierwiastków na drugi: u n + 1 = u n-1, podczas gdy u n + 2 = u n . Dla μ = 3,4 pojawiają się kolejne przybliżone wartości 0,84, 0,45, 0,84, 0,45, 0,84 ...

Poza granicą stabilności tego cyklu, √6 + 1, pojawiają się dwa nowe bifurkacje, które zależą od rozwiązań x = f (f (f (f (x)))). Dla μ = 3,47 kolejne wartości są rzędu 0,47, 0,86, 0,40, 0,84, 0,47 ...

Chaos

Od bifurkacji do bifurkacji, ewolucje stają się coraz bardziej złożone. Proces prowadzi do około μ> 3,57 w układach, w których generalnie nie ma już widocznych atraktorów. Grafika przedstawia zatem „chaotyczną” ewolucję w zwykłym znaczeniu tego terminu.

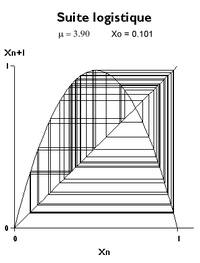
Jednak w języku matematyków słowo chaos reprezentuje silną wrażliwość na warunki początkowe. Dwa wykresy odpowiadające μ = 3,9 z wartościami początkowymi u 0 0,100 i 0,101 pokazują, że trajektorie oddalają się od siebie, aż szybko się rozróżnią. W konkretnym problemie warunki początkowe nigdy nie są dokładnie znane: po pewnym czasie chaotyczne zjawisko stało się nieprzewidywalne, mimo że definiujące je prawo jest całkowicie deterministyczne.

Załączniki

Bibliografia

• Alain Hillion , The Mathematical Theories of Populations , Paryż, Presses Universitaires de France , wyd.  „  Co ja wiem  ”1986, 127  str. , nr 2258 ( ISBN  2-13-039193-1 )
• Nicolas Bacaër , Histories of mathematics and populations , Paryż, Éditions Cassini, coll.  „Sól i żelazo”,2008, 212  s. ( ISBN  978-2-84225-101-7 , uwaga BnF n o  FRBNF42035729 ) , „Verhulst and the logistic equation”

Powiązane artykuły

• System dynamiczny
• Teoria chaosu
• Teoria ergodyczna
• Fraktal Lapunowa
• Informacje zwrotne , samoregulacja

Linki zewnętrzne

• (en) Elmer G. Wiens, Mapa logistyczna i chaos
• [PDF] Daniel Perrin, The Logistics Suite and Chaos
• (fr) Interaktywne cyfrowe doświadczenie diagramu bifurkacyjnego aplikacji logistycznej http://experiences.math.cnrs.fr

Uwagi i odniesienia

1. (w) RM May , „  Proste modele matematyczne o bardzo skomplikowanej dynamice  ” , Nature , vol.  261 n O  5.5601976, s.  459–467 ( DOI  10.1038 / 261459a0 )
2. (in) Dlaczego nie autokatalityczna i logistyczna krzywa głowicy?