Ekskluzywna funkcja OR

\ scriptstyle A \ oplus B

bez dawania

Venna z

\ scriptstyle A \ oplus B \ oplus C

$~ \ oplus ~$ $~ \ Leftrightarrow ~$

Funkcją XOR , często nazywane XOR (E x clusive ANI ) lub alternatywy wykluczają lub ⊻ w relacyjnej Algebra , to operator logiczny z logicznego Algebra . W przypadku dwóch operandów , z których każdy może mieć wartość PRAWDA lub FAŁSZ, kojarzy wynik, który sam ma wartość PRAWDA tylko wtedy, gdy oba operandy mają różne wartości.

Operator ten jest szeroko stosowany w elektronice , informatyce , a także w kryptografii ze względu na swoje ciekawe właściwości.

Jego symbolem jest tradycyjnie znak plusa w kółku: „⊕”

Definicja

Nazwijmy A i B rozważanymi dwoma operandami. Zgódźmy się przedstawić ich wartość w następujący sposób:

1 = PRAWDA
0 = FAŁSZ

Operator XOR jest definiowany przez jego tablicę prawdy , która wskazuje dla wszystkich możliwych wartości A i B wartość wyniku R:

Tabela prawdy XOR
W	b	R = A ⊕ B
0	0	0
0	1	1
1	0	1
1	1	0

Jak widać, operator logiczny XOR, czyli wykluczające OR, można zdefiniować następującym zdaniem:

Wynik jest PRAWDA, jeśli jeden i tylko jeden z operandów A i B ma wartość PRAWDA

lub

Wynik jest PRAWDA, jeśli dwa operandy A i B mają różne wartości

lub

Wynik jest PRAWDA, jeśli nieparzysta liczba wejść jest prawdziwa (ma to szczególne zastosowanie, gdy dwa lub więcej operatorów logicznych XOR jest połączonych kaskadowo (generatory bitów parzystości )

Różni się od włączającego operatora OR , ponieważ daje wynik FAŁSZ, gdy A i B są jednocześnie PRAWDA. Jego symbol różni się również od włączającego operatora OR, którego symbolem jest po prostu „PLUS”: „+”.

W przetwarzaniu danych operator ten może być użyty do połączenia dwóch bitów , z których każdy ma wartość 0 lub 1, stosując reguły zdefiniowane w poprzedniej tabeli, a sam wynik jest wartością bitu .

Z bramkami logicznymi AND / OR, A XOR B = (A AND not B) OR (nie A AND B).

Funkcja XOR jest przykładem funkcji parzystości .

Równoważność, wprowadzenie i eliminacja

Wyłączna dysjunkcja lub J pq może być wyrażona jako koniunkcja („i logiczne”, ), dysjunkcja („lub logiczna”, ) i negacja logiczna ( ) w następujący sposób: ${\ displaystyle p \ oplus q}$ $\ wedge$ $\ lor$ $\ lnot$

{\ Displaystyle {\ rozpocząć {macierz} p \ oplus q & = & (p \ lor q) \ ziemia \ lnot (p \ ziemia q) \ koniec {macierz}}}

Wyłączną dysjunkcję można również sformułować w następujący sposób: ${\ displaystyle p \ oplus q}$

{\ Displaystyle {\ rozpocząć {macierz} p \ oplus q & = & (p \ ziemia \ lnot q) \ lor (\ lnot p \ ziemia q) \ koniec {macierz}}}

Ta reprezentacja XOR może być przydatna podczas budowania obwodu lub sieci, ponieważ ma tylko jedną operację i niewielką liczbę operacji i . Dowód tej tożsamości podano poniżej: $\ lnot$ $\ wedge$ $\ lor$

{\ Displaystyle {\ rozpocząć {macierz} p \ oplus q & = & (p \ ziemia \ lnot q) & \ lor & (\ lnot p \ ziemia q) \\ [3pt] & = & ((p \ ziemia \ lnot q) \ lor \ lnot p) & \ land & ((p \ land \ lnot q) \ lor q) \\ [3pt] & = & ((p \ lor \ lnot p) \ land (\ lnot q \ lor \ lnot p)) & \ land & ((p \ lor q) \ land (\ lnot q \ lor q)) \\ [3pt] & = & (\ lnot p \ lor \ lnot q) & \ land & (p \ lor q) \\ [3pt] & = & \ lnot (p \ land q) & \ land & (p \ lor q) \ end {matrix}}}

Czasami warto zauważyć, co następuje:

{\ displaystyle p \ oplus q}

{\ Displaystyle {\ rozpocząć {macierz} p \ oplus q & = & \ lnot ((p \ ziemia q) \ lor (\ lnot p \ ziemia \ lnot q)) \ koniec {macierz}}}

lub:

{\ Displaystyle {\ rozpocząć {macierz} p \ oplus q & = & (p \ lor q) \ ziemia (\ lnot p \ lor \ lnot q) \ koniec {macierz}}}

Tę równoważność można ustalić, stosując prawa De Morgana dwukrotnie do czwartej linii powyższego dowodu.

Wyłączność lub jest również równoważna zaprzeczeniu równoważności logicznej przez reguły implikacji materialnej.

Podsumowując, mamy:

{\ Displaystyle {\ rozpocząć {macierz} p \ oplus q & = & (p \ ziemia \ lnot q) & \ lor & (\ lnot p \ ziemia q) & = & p {\ overline {q}} + {\ overline {p}} q \\ [3pt] & = & (p \ lor q) & \ land & (\ lnot p \ lor \ lnot q) & = & (p + q) ({\ overline {p}} + {\ overline {q}}) \\ [3pt] & = & (p \ lor q) & \ land & \ lnot (p \ land q) & = & (p + q) ({\ overline {pq} }) \ end {matrix}}}

Niektóre właściwości matematyczne

$A \ oplus A = 0$ (można łatwo sprawdzić w tabeli 2 możliwe wartości A )
$A \ oplus 0 = A$
$A \ oplus 1 = {\ bar {A}}$
$A \ oplus {\ bar {A}} = 1$
Przemienność $A \ oplus B = B \ oplus A$
Łączność, gdzie jest funkcja koincydencji. ${\ Displaystyle A \ oplus (B \ oplus C) = (A \ oplus B) \ oplus C = A \ odot (B \ odot C) = (A \ odot B) \ odot C}$ $\ odot$
${\ Displaystyle A \ oplus B = (A + B) \ oplus A \ cdot B}$
$A \ oplus B = 0$ wtedy i tylko wtedy (w pewnym sensie, jest natychmiastowe, w drugiej, przy użyciu właściwości skojarzeń i własności: ) $A = B.$ $A \ oplus 0 = A$
${\ Displaystyle A \ oplus B = {\ bar {A}} \ cdot B + A \ cdot {\ bar {B}}}$ Wyprowadzamy z tej własności: a nawet jeszcze raz: i jeszcze raz: ${\ Displaystyle {\ overline {A \ oplus B}} = A \ cdot B + {\ bar {A}} \ cdot {\ bar {B}}}$ $\ overline {A \ oplus B} = \ overline A \ oplus B = A \ oplus \ overline B$ $A \ oplus B = \ overline A \ oplus \ overline B$
$A \ oplus B = C$ tak i $C \ oplus B = A$ $A \ oplus C = B$
$(A \ oplus B) \ oplus B = A$ (Konsekwencja pierwszych dwóch właściwości i asocjatywności - przydatne w kryptografii (patrz poniżej))
Zbiór {0; 1} wyposażony w dwa prawa wewnętrznego składu wyłączny OR i AND jest ciałem skończonym .

Przykład zastosowania w kryptografii

Rozważ, że dokument cyfrowy ma być zaszyfrowany, składa się z szeregu bitów . W metodzie szyfrowania strumieniowego musi również istnieć seria bitów o tej samej długości, całkowicie losowych , nazywana kluczem szyfrowania . Bity dokumentu są przetwarzane jeden po drugim, łącząc go z bitem o tej samej randze klucza szyfrującego.

Nazwijmy się wyraźny bit i B nieco o tej samej rangi w kolejności losowej.

Szyfrowanie jest do obliczania bitu C przez C = A ⊕ B . C jest szyfrowana .

Odszyfrować C ponownie stosując bitów B w dowolnej kolejności i obliczono: C ⊕ B .

Wynikiem jest A , czysty bit, ponieważ C ⊕ B = A ⊕ B ⊕ B = A ⊕ 0 = A , używając dwóch pierwszych właściwości powyżej.

Ta metoda jest jednym ze sposobów wykonywania szyfrowania symetrycznego , w którym ten sam klucz jest używany do szyfrowania i odszyfrowywania.

Ten system, chociaż w zasadzie bardzo prosty, może okazać się nienaruszalny, jeśli sekwencja bitów klucza jest naprawdę losowa. Tej ostatniej też trzeba użyć tylko raz (mówimy o jednorazowej masce , a nawet „jednorazowej podkładce”). W tym zdaniu najtrudniejsze do zrealizowania okazuje się przede wszystkim słowo „losowe”. Ale kiedy klucz jest naprawdę losowy (technicznie rzecz biorąc, jest rysowany zgodnie z równomiernym rozkładem między wszystkimi możliwymi sekwencjami tej długości), system ten jest całkowicie bezpieczny, w pewnym sensie rygorystycznie zdefiniowany przez Claude'a Shannona w 1949 roku w artykule założyciel "Komunikacyjna teoria systemów tajnych". Należy dodać, że jest to jedyne szyfrowanie dające w teorii absolutne bezpieczeństwo.

Zobacz także artykuł: maska jednorazowa

Rysunek

Oto numeryczny przykład poprzedniej metody:

M = 0110101011010100 (wiadomość tekstowa)

K = 0101011011100110 (klucz; oczywiście należy go zachować w tajemnicy)

Umówmy się, że symbol ⊕ reprezentuje tutaj zastosowanie operatora XOR do każdego z bitów

Aby zaszyfrować, musisz użyć tabeli prawdy: „M” to Twoja wiadomość, a „K” to tajny klucz.

A więc: M ⊕ K = C. „C” oznacza zaszyfrowaną wiadomość:

Szyfrowanie: C = M ⊕ K = 0011110000110010 (zaszyfrowana wiadomość)

Deszyfrowanie: M = C ⊕ K = 0110101011010100 (odszyfrowana wiadomość)

Historia

Ten system szyfrowania był używany w czerwonym telefonie , a właściwie teleksie , bezpośrednio łączącym Kreml z Białym Domem , a klucze przechodziły następnie przez torby dyplomatyczne . System jednorazowych masek był również używany przez sowieckich szpiegów. Niektóre maski były używane więcej niż raz (czasami z przerwami w latach), co pozwoliło usługom szyfrującym w języku angielskim na odszyfrowanie pewnych wiadomości.

Inne zastosowania w kryptografii

Wszystkie szyfry symetryczne używają operatora XOR. W szczególności symetryczny algorytm kryptograficzny o wysokim poziomie bezpieczeństwa AES ( Rijndael ) wykorzystuje bardzo dużą ich liczbę.

Zastosowanie w elektronice

Przykład zastosowania: Układ scalony 7486 TTL lub układ scalony CMOS 4070 integruje cztery bramki logiczne ekskluzywnego typu OR. Ilustracja: Przykład: Lampka zapala się po naciśnięciu tylko „a” lub „b”, ale nie po jednoczesnym naciśnięciu „a” i „b”.

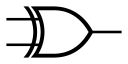
Diagram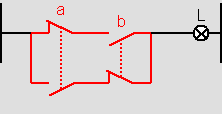

Równanie

L = a \ oplus b

L = ({\ bar {a}}. B) + (a. {\ Bar {b}})

Chronogram

Symbol IEC

Symbol ANSI (zwany także wojskowym)

Aplikacje komputerowe

Oprócz zastosowań związanych z kryptografią, wyłączna funkcja OR pozwala szybko zresetować wartość zmiennej (często rejestru ) do zera.

Weźmy na przykład kod asemblera, który używa wyłącznego OR, aby zresetować wartość rejestru eax do zera:

xor eax, eax

Na procesorach typu x86 ta instrukcja jest krótsza (pod względem liczby bajtów) niż następujący intuicyjny kod:

mov eax, 0

Pozwala również na zerowanie zmiennej, gdy warunki nie pozwalają na bajt 0x00 w binarnym ( kodzie powłoki ).

Możesz również użyć wyłącznego OR, aby wymienić dwie zmienne bez użycia zmiennej tymczasowej .

Zastosowanie w domowej elektryczności

Jedna aplikacja używana przez wyłącznego operatora logicznego OR w domowych instalacjach elektrycznych znajduje się w pomieszczeniach, w których żarówkę można włączać i wyłączać za pomocą dwóch przełączników umieszczonych w pobliżu dwóch wejść. Każdy z dwóch przełączników może włączać lub wyłączać żarówkę, niezależnie od położenia drugiego przełącznika. Aby uzyskać taką funkcjonalność, musimy połączyć dwa przełączniki, tworząc operator XOR. Jest to tak zwane zgromadzenie „ tam iz powrotem ”.